数据分析
数据分析是为了提取有用信息并形成一定的结论,而对收集来的数据通过一定的统计分析方法进行分析的过程。
数据分析的数学基础在20世纪初就已确立,到计算机的出现后,计算能力的飞速发展使得数据分析也得到了蓬勃的发展。

常用数据分析方法
1.聚类分析(Cluster Analysis)
聚类分析指将物理或抽象对象的集合分组成为由类似的对象组成的多个类的分析过程。聚类分析又称群分析,是根据“物以类聚”的道理,对样品或指标进行分类的一种多元统计分析方法。
聚类分析按照个体或样品(individuals, objects or subjects)的特征将它们分类,使同一类别内的个体具有尽可能高的同质性(homogeneity),而类别之间则应具有尽可能高的异质性(heterogeneity)。
聚类分析是一种探索性的分析,在分类的过程中,人们不必事先给出一个分类的标准,聚类分析能够从样本数据出发,自动进行分类。聚类分析所使用方法的不同,常常会得到不同的结论。不同研究者对于同一组数据进行聚类分析,所得到的聚类数未必一致。
聚类分析的应用范围比较广,例如在电子商务网站中,通过分组聚类出具有相似浏览行为的客户,并分析客户的共同特征,可以更好的帮助电子商务网站了解自己的客户,向客户提供更合适的服务。
聚类分析计算方法主要有如下几种: - 分裂法(partitioning methods),首先创建k个划分,k为要创建的划分个数;然后利用一个循环定位技术通过将对象从一个划分移到另一个划分来帮助改善划分质量。 - 层次法(hierarchical methods),创建一个层次以分解给定的数据集。该方法可以分为自上而下(分解)和自下而上(合并)两种操作方式。为弥补分解与合并的不足,层次合并经常要与其它聚类方法相结合,如循环定位。 - 基于密度的方法(density-based methods),根据密度完成对象的聚类。它根据对象周围的密度(如DBSCAN)不断增长聚类。 - 基于网格的方法(grid-basedmethods),首先将对象空间划分为有限个单元以构成网格结构;然后利用网格结构完成聚类。 - 基于模型的方法(model-based methods),它假设每个聚类的模型并发现适合相应模型的数据。
2.因子分析(Factor Analysis)
因子分析是指研究从变量群中提取共性因子的统计技术。因子分析就是从大量的数据中寻找内在的联系,减少决策的困难。
因子分析的主要目的是用来描述隐藏在一组测量到的变量中的一些更基本的,但又无法直接测量到的隐性变量 (latent variable, latent factor)。
因子分析应用范围很广,例如在用户行为研究中的问卷调查就是一个典型应用,可以通过分析反应用户的一些喜好。
因子分析的方法约有10多种,如重心法、影像分析法,最大似然解、最小平方法、阿尔发抽因法、拉奥典型抽因法等等。这些方法本质上大都属近似方法,是以相关系数矩阵为基础的,所不同的是相关系数矩阵对角线上的值,采用不同的共同性估值。在社会学研究中,因子分析常采用以主成分分析为基础的反覆法。
3.相关分析(Correlation Analysis)
相关分析(correlation analysis),相关分析是研究现象之间是否存在某种依存关系,并对具体有依存关系的现象探讨其相关方向以及相关程度。
相关关系是一种非确定性的关系,例如,以X和Y分别记一个人的身高和体重,或分别记每公顷施肥量与每公顷小麦产量,则X与Y显然有关系,而又没有确切到可由其中的一个去精确地决定另一个的程度,这就是相关关系。
相关性分析的应用示例,比如多种股票的相关性分析为投资者提供很多有用的参考。
4.对应分析(Correspondence Analysis)
对应分析(Correspondence analysis)也称关联分析、R-Q型因子分析,通过分析由定性变量构成的交互汇总表来揭示变量间的联系。
可以揭示同一变量的各个类别之间的差异,以及不同变量各个类别之间的对应关系。对应分析的基本思想是将一个联列表的行和列中各元素的比例结构以点的形式在较低维的空间中表示出来。
应用主要集中在市场定位和细分的研究。
5.回归分析
研究一个随机变量Y对另一个(X)或一组(X1,X2,…,Xk)变量的相依关系的统计分析方法。回归分析(regression analysis)是确定两种或两种以上变数间相互依赖的定量关系的一种统计分析方法。
回归分析运用十分广泛,回归分析按照涉及的自变量的多少,可分为一元回归分析和多元回归分析;按照自变量和因变量之间的关系类型,可分为线性回归分析和非线性回归分析。
回归分析的应用示例,比如常见的质量和满意度分析。
6.方差分析(ANOVA/Analysis of Variance)
又称“变异数分析”或“F检验”,是R.A.Fisher发明的,用于两个及两个以上样本均数差别的显著性检验。由于各种因素的影响,研究所得的数据呈现波动状。造成波动的原因可分成两类,一是不可控的随机因素,另一是研究中施加的对结果形成影响的可控因素。
方差分析是从观测变量的方差入手,研究诸多控制变量中哪些变量是对观测变量有显著影响的变量。
方差分析的范围很广,比如分析一下不同的手机代工厂质量情况。
数据分析常用的图表方法
1.排列图(柏拉图)
排列图是分析和寻找影响质量主原因素的一种工具,其形式用双直角坐标图,左边纵坐标表示频数(如件数金额等),右边纵坐标表示频率(如百分比表示)。分折线表示累积频率,横坐标表示影响质量的各项因素,按影响程度的大小(即出现频数多少)从左向右排列。通过对排列图的观察分析可抓住影响质量的主原因素。

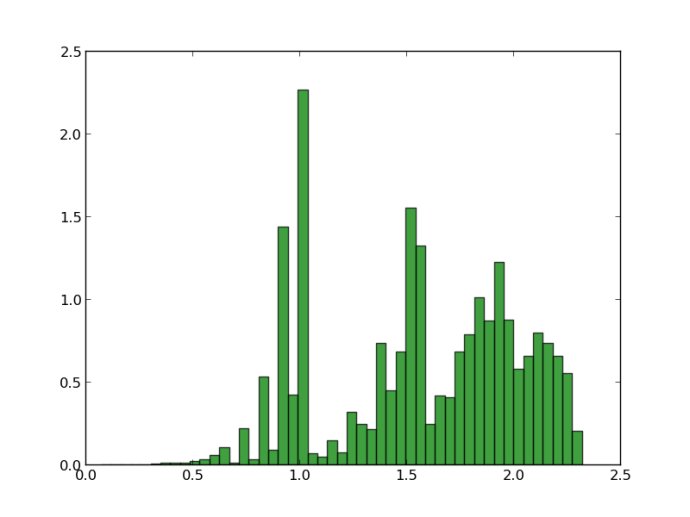
2.直方图
将一个变量的不同等级的相对频数用矩形块标绘的图表(每一矩形的面积对应于频数)。
直方图(Histogram)又称柱状图、质量分布图。是一种统计报告图,由一系列高度不等的纵向条纹或线段表示数据分布的情况。 一般用横轴表示数据类型,纵轴表示分布情况。
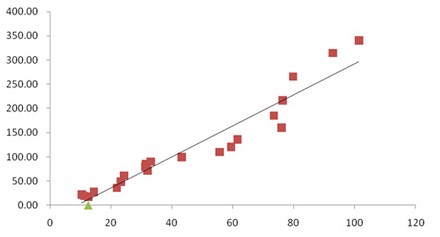
3.散点图(scatter diagram)
散点图表示因变量随自变量而变化的大致趋势,据此可以选择合适的函数对数据点进行拟合。用两组数据构成多个坐标点,考察坐标点的分布,判断两变量之间是否存在某种关联或总结坐标点的分布模式。
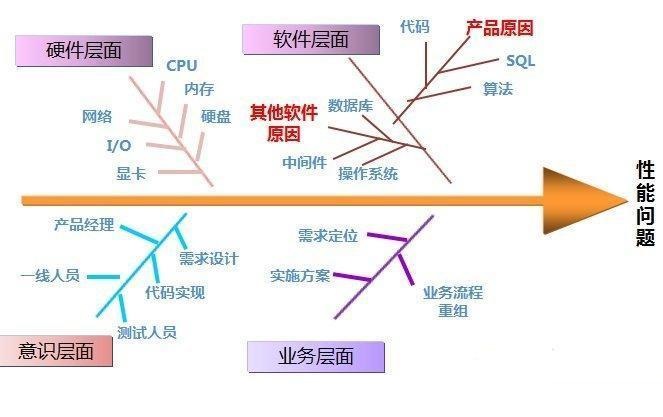
4.鱼骨图(Ishikawa)
鱼骨图是一种发现问题“根本原因”的方法,它也可以称之为“因果图”。其特点是简捷实用,深入直观。它看上去有些象鱼骨,问题或缺陷(即后果)标在”鱼头”外。
5.FMEA
FMEA是一种可靠性设计的重要方法。它实际上是FMA(故障模式分析)和FEA(故障影响分析)的组合。它对各种可能的风险进行评价、分析,以便在现有技术的基础上消除这些风险或将这些风险减小到可接受的水平。
数据分析统计工具
1.SPSS。
SPSS是世界上最早采用图形菜单驱动界面的统计软件,它最突出的特点就是操作界面极为友好,输出结果美观漂亮。它将几乎所有的功能都以统一、规范的界面展现出来,使用Windows的窗口方式展示各种管理和分析数据方法的功能,对话框展示出各种功能选择项。用户只要掌握一定的Windows操作技能,粗通统计分析原理,就可以使用该软件为特定的科研工作服务。
2.minitab。
MINITAB功能菜单包括:假设检验(参数检验和非参数检验),回归分析(一元回归和多元回归、线性回归和非线性回归),方差分析(单因子、多因子、一般线性模型等),时间序列分析,图表(散点图、点图、矩阵图、直方图、茎叶图、箱线图、概率图、概率分布图、边际图、矩阵图、单值图、饼图、区间图、Pareto、Fishbone、运行图等)、蒙特卡罗模拟和仿真、SPC(Statistical Process Control -统计过程控制)、可靠性分析(分布拟合、检验计划、加速寿命测试等)、MSA(交叉、嵌套、量具运行图、类型I量具研究等)等。
3.JMP。
JMP的算法源于SAS,特别强调以统计方法的实际应用为导向,交互性、可视化能力强,使用方便,尤其适合非统计专业背景的数据分析人员使用,在同类软件中有较大的优势。JMP的应用领域包括业务可视化、探索性数据分析、六西格玛及持续改善(可视化六西格玛、质量管理、流程优化)、试验设计、生存及可靠性、统计分析与建模、交互式数据挖掘、分析程序开发等。JMP是六西格玛软件的鼻祖,当年摩托罗拉开始推六西格玛的时候,用的就是JMP软件,目前有非常多的全球顶尖企业采用JMP作为六西格玛软件,包括陶氏化学、惠而浦、铁姆肯、招商银行、美国银行、中国石化等等。