椭圆曲线密码学是下一代的公钥密码学,它比之前的公钥密码学 系统例如RSA和Diffe-Hellman在安全性方面有显著提高。 椭圆曲线密码学是目前被广泛使用的最强大的密码学算法之一,但是 真正理解其工作原理的开发者并不多。
1、椭圆曲线方程
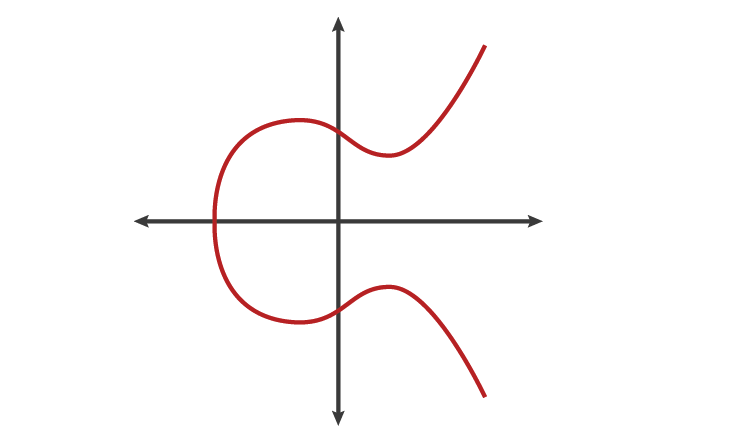
椭圆曲线有一系列满足特定数学方程的点组成。一个椭圆曲线的方程看起来 像这样:
Y² = X³ + ax + b
也有其他的椭圆曲线表达式,从技术上来将,一个椭圆曲线就是由满足 上述方程的点组成,它的一些固有的特征使其非常适合用于密码学。
上面的曲线有很多有趣的特性,其中之一就是水平对称性。椭圆曲线上 的任何一个点关于X轴的对称点依然还在曲线上。另一个更有意思的特性 是,任何一条不垂直于X轴的直线与椭圆曲线的交点不会超过3个。 假设我们从椭圆曲线上任选两个点画一条直线,那么这条直线将在 第三个点与椭圆曲线相交。
可以把这个过程想象成一个台球游戏,如果你在A点拿一个球向B点射击, 当这个球碰到曲线后,就会弹向下方(如果球在X轴上方)或上方(如果 球在X轴下方),就像下面这张动图:
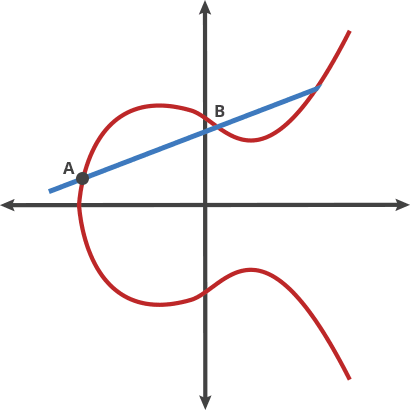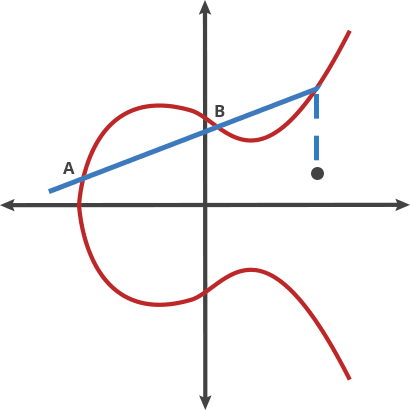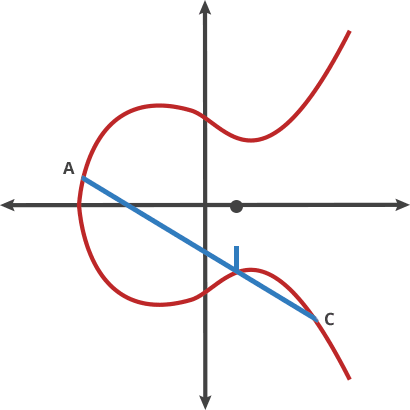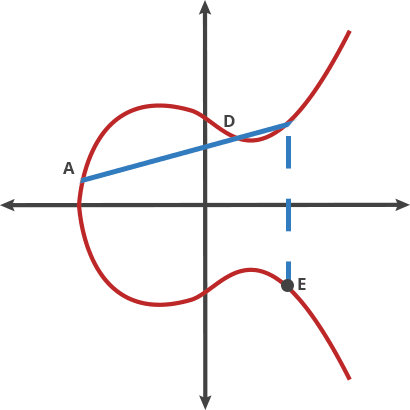
如果将台球在这两点上的运动称为dot运算,那么椭圆曲线上任何两点 都可以进行dot运算:
1 | A dot B = C |
现在,如果你有两个点,一个初始点和自己dot运算n次后到达终止的点, 那么当你只知道这个终止点和初始点的时候,要找出这个n具体是多少是 非常困难的。
假设一个人自己在屋里玩台球,他可以按照上面的规则一遍遍的击球, 过一会儿进来另一个人看到了台球的当前位置,那么即使他知道游戏规则 以及开始时球的位置,也无法确定到底击打了多少次球。唯一的办法就是 自己重玩游戏并试着让球到达同样的位置。

2、素数椭圆曲线
我们看到的椭圆曲线是一个简化版本,它对于解释椭圆曲线的工作原理很有 帮助,不过和密码学中实际用到的曲线还有比较大的差距。
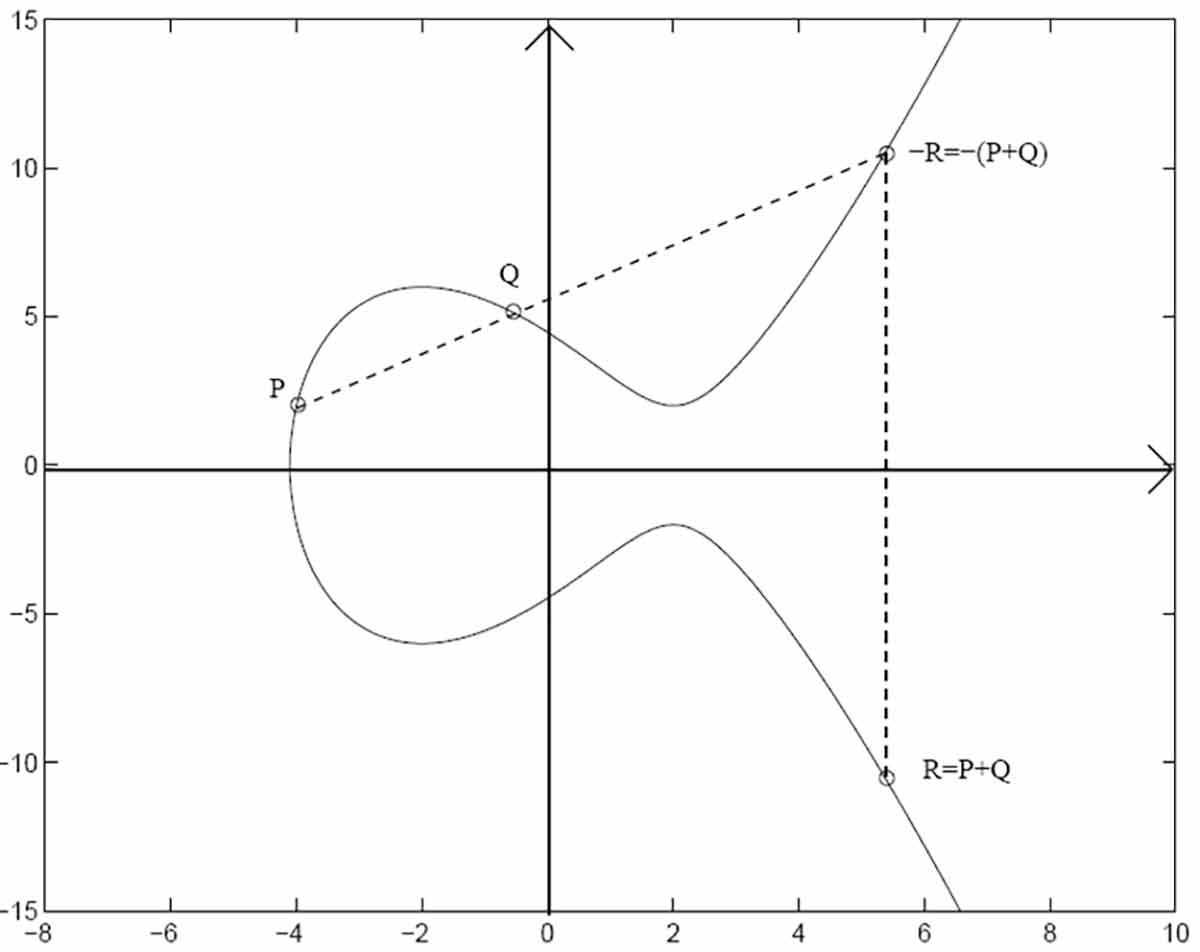
将椭圆曲线用于密码学需要首先将取值范围限定到有限区间,就像RSA里 那样,我们只允许一个固定区间内的整数,如果数值超过了这个区间的最大 值,就取模。如果我们选择一个素数作为区间最大值,那么这个椭圆曲线 就被称为素数曲线并同时具有了令人难以置信的密码学特性。
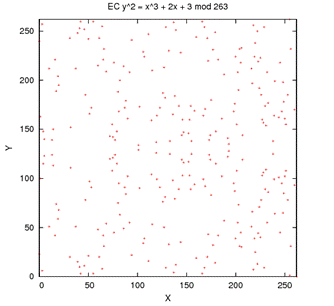
虽然上图看起来不像传统意义上的曲线,它的确是,它是原始的椭圆曲线 被限定在指定的区间内并且取整的结果,你能看到关于X轴的对称性 依然存在。
回到我们的台球游戏,前面的dot运算对这个离散曲线依然适用。曲线 上的直线方程依然也还有同样的性值。更令人激动的是离散曲线上的dot 运算可以更高效的计算。当两点连成的直线碰到边界后会转到另一边继续 前进,直到碰到一个点:

有了这些新的工具,我们可以进行一些密码学操作了。假设你有 一条消息,将其设为x坐标,然后求出来曲线上对应点的y坐标。
输出就是 : (71, 6), “-”, (78, 44), (80, 4), 64, 24)
椭圆曲线离散对数是一个难题,这是椭圆曲线密码学的根基。虽然已经 三个世纪的数学研究,目前还没有找到什么算法可以比原始求解更有效。 和素数分解不同,基于目前的数学知识,不存在可以缩小门限函数差距 的捷径。这意味着对于相同大小的数值,求解椭圆曲线离散对数要远远 难于素数分解,这也意味着椭圆曲线密码学系统要比RSA或Diffe-Hellman 更难攻破。
适用椭圆曲线密码学,你可以用较小的密钥获得同样的安全等级。小 密钥变得越来越重要,尤其是今天有越来越多的密码学计算是在手机和IOT 设备之类的不那么强大的设备上运行的。
原文链接:Elliptic Curve Cryptography For Those Who Hate Maths
汇智网翻译整理,转载请标明出处